Dalam istilah ilmu komputer, sebuah struktur data adalah cara penyimpanan, penyusunan dan pengaturan data di dalam media penyimpanan komputer sehingga data tersebut dapat digunakan secara efisien.
Dalam teknik pemrograman, struktur data berarti tata letak data yang berisi kolom-kolom data, baik itu kolom yang tampak oleh pengguna (
user) atau pun kolom yang hanya digunakan untuk keperluan pemrograman yang tidak tampak oleh pengguna. Setiap baris dari kumpulan kolom-kolom tersebut dinamakan catatan (
record). Lebar kolom untuk data dapat berubah dan bervariasi. Ada kolom yang lebarnya berubah secara dinamis sesuai masukan dari pengguna, dan juga ada kolom yang lebarnya tetap. Dengan sifatnya ini, sebuah struktur data dapat diterapkan untuk pengolahan database (misalnya untuk keperluan data keuangan) atau untuk pengolah kata (
word processor) yang kolomnya berubah secara dinamis. Contoh struktur data dapat dilihat pada berkas-berkas lembar-sebar (
spreadsheet), pangkal-data (
database), pengolahan kata, citra yang dipampat (dikompres), juga pemampatan berkas dengan teknik tertentu yang memanfaatkan struktur data.
1. Larik (Array)
Larik (Bahasa Inggris:
array), dalam ilmu komputer, adalah suatu tipe data terstruktur yang dapat menyimpan banyak data dengan suatu nama yang sama dan menempati tempat di memori yang berurutan (kontinu) serta bertipe data sama pula.
Larik dapat diakses berdasarkan indeksnya. Indeks larik umumnya dimulai dari 0 dan ada pula yang dimulai dari angka bukan 0. Pengaksesan larik biasanya dibuat dengan menggunakan perulangan (
looping).
Larik satu dimensi merupakan jenis larik dasar dan jenis larik yang paling sering digunakan, pemakaian larik satu dimensi terutama dipakai dalam tipe data string (terutama dalam bahasa Bahasa pemrograman C).
Larik dua dimensi merupakan tipe larik yang lain. Larik dua dimensi sering dipakai untuk merepresentasikan tabel dan matriks dalam pemrograman.
Larik dalam beberapa bahasa pemrograman
Larik dalam bahasa Pascal dapat didefinisikan dengan indeks awal dan indeks akhirnya.
Contoh:
program larik;
var arr: array[1..10] of integer; //larik dengan indeks awal 1 dan indeks akhir 10
begin
arr[1] := 5; //memasukkan nilai ke indeks 1
writeln(arr[i]); //mencetak angka 5
end.
Larik dalam bahasa C selalu dimulai dari indeks 0. Larik dapat didefinisikan secara statik atau dinamik. Jika didefinisikan statik, ukuran larik akan tetap dari awal program hingga akhir program. Jika didefinisikan dinamik, ukuran larik dapat berubah selama program berjalan karena memesan tempat pada memori heap. Proses pemesanan tempat pada memori disebut dengan alokasi. Sedangkan proses pembebasan memori yang sudah dipesan disebut dengan dealokasi.
Contoh larik statik:
#include <stdio.h>
int main(){
int arr[10]; //indeks awal 0 dan indeks akhir 9
arr[0] = 5;
printf(“%d\n”, arr[0]);
}
Contoh larik dinamik:
#include <malloc.h>
int main(){
int * arr;
arr = (int *) malloc(10 * sizeof(int)); //memesan 10 tempat pada memori
arr[0] = 5;
free(arr); //menghancurkan larik. Memori pada heap dibebaskan
arr = (int *) malloc(5 * sizeof(int)); //memesan 5 tempat baru pada memori
free(arr); //di akhir program jangan lupa untuk menghancurkan larik dinamik
}
Dalam bahasa Java tipe data larik direpresentasikan sebagai sebuah objek khusus. Karena itu pada bahasa Java larik yang dibuat selalu bersifat dinamik. Namun walaupun bersifat dinamik, larik pada bahasa Java tidak perlu dihancurkan karena proes penghancuran dilakukan secara otomatis melalui suatu prosedur yang disebut dengan Pengumpulan sampah (Inggris:
Garbage Collecting). Sama seperti bahasa C, indeks larik selalu dimulai dari 0.
Contoh:
public class larik {
public static void main(String args[]) {
int[] arr = new arr[10];
arr[0] = 5;
System.out.println(arr[0]);
}
}
Sama seperti di JAVA larik di PHP juga merupakan sebuah object lebih tepatnya lagi map terorder. Ada dua tipe larik di PHP,
indexed array (
simple array) dan a
ssociated array (
value array). Di PHP, element larik bisa berupa string, Bilangan, boolean, dan semua tipe data primitif lainnya, termasuk larik juga bisa menjadi element larik lainnya.
Cara medefinisikan larik:
#mendefinisikan array kosong
$larik = array();
Contoh indexed array (simple array):
$jam = array(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12);
$hari = array(‘senin’, ‘selasa’, ‘selasa’, ‘rabu’, ‘kamis’, ‘jumat’, ‘sabtu’);
Contoh associated array:
$bulan = array(’1′=>’January’, ’2′=>’February’, ’3′=>’Maret’, ’4′=>’April’);
$komponenKalender = array(
‘bulan’=> array(1, 2, 3, 4, 5, 6, 7, 8, 9 ,10 , 11, 12),
‘hari’ => array(‘senin’, ‘selasa’, ‘selasa’, ‘rabu’, ‘kamis’, ‘jumat’, ‘sabtu’)
);
2. Stack (Tumpukan)
Dalam ilmu komputer, stack atau tumpukan merupakan sebuah koleksi objek yang menggunakan prinsip
LIFO (Last In First Out), yaitu data yang terakhr kali dimasukkan akan pertama kali keluar dari stack tersebut. Stack dapat diimplementasikan sebagai representasi berkait atau kontigu (dengan tabel fix). Ciri Stack :
* Elemen TOP (puncak) diketahui
* penisipan dan penghapusan elemen selalu dilakukan di TOP
* LIFO
Pemanfaatan Stack :
* Perhitungan ekspresi aritmatika (posfix)
* algoritma backtraking (runut balik)
* algoritma rekursif
Operasi Stack yang biasanya :
a. Push (input E : typeelmt, input/output data : stack): menambahkan sebuah elemen ke stack
b. Pop (input/output data : stack, output E : typeelmt ) : menghapus sebuah elemen stack
c. IsEmpty ()
d. IsFull ()
e. dan beberapas selektor yang lain
3. Pohon (Tree)
Dalam ilmu komputer, sebuahPohon adalah suatu struktur data yang digunakan secara luas yang menyerupai struktur pohon dengan sejumlah simpul yang terhubung.
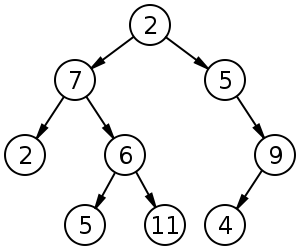
Sebuah Simpul dapat mengandung sebuah nilai atau suatu kondisi atau menggambarkan sebuah struktur data terpisah atau sebuah bagian pohon itu sendiri. Setiap simpul dalam sebuah pohon memiliki nol atau lebih simpul anak (
child nodes), yang berada dibawahnya dalam pohon (menurut perjanjian, pohon berkembang ke bawah, tidak seperti yang dilakukannya di alam). Sebuah simpul yang memiliki anak dinamakan simpul ayah (
parent node) atau simpul leluhur (
ancestor node) atau superior. Sebuah simpul paling banyak memiliki satu ayah. Tinggi dari pohon adalah panjang maksimal jalan ke sebuah daun dari simpul tersebut. Tinggi dari akar adalah tinggi dari pohon. Kedalaman dari sebuah simpul adalah panjang jalan ke akarnya dari simpul tersebut.
Simpul yang paling atas dalam pohon adalah akar (
root node). Menjadi simpul teratas, simpul akar tidak akan memiliki orang tua. Ini merupakan simpul di mana biasanya merupakan tempat untuk memulai operasi dalam pohon (walaupun beberapa algoritma dimulai dengan daun dan berakhir pada akar). Semua simpul yang lain dapat dicapai dari akar dengan menelusuri pinggiran atau pranala. (Dalam definisi resmi, setiap jalan adalah khas). Dalam diagram, ini secara khusus di gambar paling atas. Di beberapa pohon, seperti heap, akar memiliki sifat khusus. Setiap simpul dalam sebuah pohon dapat dilihat sebagai akar dari sub pohon yang berakar pada simpul tersebut.
Semua simpul yang berada pada tingkat terendah dari pohon dinamakan daun (
leaf node). Sejak mereka terletak pada tingkat paling bawah, mereka tidak memiliki anak satupun. Seringkali, daun merupakan simpul terjauh dari akar. Dalam teori grafik, sebuah daun adalah sebuah sudut dengan tingkat 1 selain akar (kecuali jika pohonnya hanya memiliki satu sudut; maka akarnya adalah daunnya juga). Setiap pohon memiliki setidaknya satu daun. Dalam pohon berdasarkan genetic programming sebuah daun (juga dibilang terminal) adalah bagian terluar dari sebuah program pohon. Jika dibandingkan dengan fungsinya atau simpul dalam, daun tidak memiliki argumen. Di banyak kasus dalam daun-GP input ke programnya.

- Simpul dalam (Internal nodes)
Sebuah simpul dalam adalah semua simpul dari pohon yang memiliki anak dan bukan merupakan daun. Beberapa pohon hanya menyimpan data didalam simpul dalam, meskipun ini mempengaruhi dinamika penyimpanan data dalam pohon. Sebegai contoh, dengan daun yang kosong, seseorang dapat menyimpan sebuah pohon kosong dengan satu daun. Bagaimanapun juga dengan daun yang dapat menyimpan data, tidak dimungkinkan untuk menyimpan pohon kosong kecuali jika seseorang memberikan beberapa jenis penanda data di daun yang menandakan bahwa daun tersebut seharusnya kosong (dengan demikian pohon itu seharusnya kosong juga). Sebaliknya, beberapa pohon hanya menyimpan data dalam daun, dan menggunakan simpul dalam untuk menampung metadata yang lain, seperti jarak nilai dalam sub pohon yang berakar pada simpul tersebut. Jenis pohon ini berguna untuk jarak yang meragukan.
Sebuah sub pohon adalah suatu bagian dari pohon struktur data yang dapat dilihat sebagai sebuah pohon lain yang berdiri sendiri. Simpul apapun dalam pohon P, bersama dengan seluruh simpul dibawahnya, membentuk sebuah sub pohon dari P. Sub pohon yang terhubung dengan akar merupakan keseluruhan pohon tersebut. Sub pohon yang terhubung dengan simpul lain manapun dinamakan sub pohon asli (
proper subtree).
Terdapat dua jenis pohon. Sebuah pohon tidak terurut (unordered tree) adalah sebuah pohon dalam arti struktural semata-mata, yang dapat dikatakan memberikan sebuah simpul yang tidak memiliki susunan untuk anak dari simpul tersebut. Sebuah pohon dengan suatu susunan ditentukan, sebagai contoh dengan mengisi bilangan asli berbeda ke setiap anak dari simpul tersebut, dinamakan sebuah pohon terurut (ordered tree), dan struktur data yang dibangun didalamnya dinamakan pohon terurut struktur data (
ordered tree data structures). Sejauh ini pohon terurut merupakan bentuk umum dari pohon struktur data. Pohon biner terurut merupakan suatu jenis dari pohon terurut.
Sebuah hutan adalah sebuah himpunan yang terdiri dari pohon terurut. Lintasan inorder, preorder, dan postorder didefinisikan secara rekursif untuk hutan.
- inorder
1. lewati inorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
2. kunjungi akar dari pohon pertama.
3. lewati inorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.
- preorder
1. kunjungi akar dari pohon pertama.
2. lewati preorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
3. lewati preorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.
- postorder
1. lewati postorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
2. lewati postorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.
3. kunjungi akar dari pohon pertama.
Ada banyak cara untuk menggambarkan pohon; pada umumnya penggambaran mewakili simpul sebagai rekor yang dialokasikan pada heap (bedakan dengan heap struktur data) yang mengacu pada anaknya, ayahnya, atau keduanya, atau seperti data materi dalam array, dengan hubungan diantaranya ditentukan oleh posisi mereka dalam array (contoh binary heap).
Dalam teori grafik, sebuah pohon adalah sebuah grafik asiklis yang terhubung. Pohon yang berakar merupakan sebuah grafik dengan sudut tunggal diluar sebagai akar. Dalam kasus ini, dua sudut apapun yang terhubung dengan sebuah sisi mewarisi hubungan orang tua dan anak. Sebuah grafik asiklis dengan bermacam-macam komponen yang terhubung atau himpunan dari pohon-pohon yang berakar kadang-kadang dipanggil hutan.
Melangkah melalui materi dari pohon, dengan arti dari hubungan antara orang tua dan anak, dinamakan menelusuri pohon, dan tindakannya adalah sebuah jalan dari pohon. Seringkali, sebuah operasi mungkin dapat dilakukan sebagai penunjuk ysng mengacu pada simpul khusus. Sebuah penelusuran dimana setiap simpul ayah dikunjungi sebelum anaknya dinamakan
pre-order walk, yaitu sebuah penelusuran dimana anaknya dikunjungi sebelum ayahnya masing-masing dinamakan post-order walk.
* Menghitung seluruh materi (item)
* Pencarian untuk sebuah materi
* Menambahkan sebuah materi pada sebuah posisi tertentu dalam pohon
* Menghapus sebuah materi
* Mengeluarkan seluruh bagian dari sebuah pohon pruning
* Menambahkan seluruh bagian ke sebuah pohon grafting
* Menemukan akar untuk simpul apapun
* Memanipulasi data secara hierarki
* Membuat informasi mudah untuk dicari
* Memanipulasi data sorted lists


mantap bung
BalasHapusMy blog
terimakasih pembelajaran nya
BalasHapusMy blog
My Campus